Ukládáme hierarchická data v databázi – II

V minulém díle miniseriálu jsme si osvěžili klasickou metodu ukládání stromů do databáze tak, jak ji každý z nás zná. Dnes se podíváme na tzv. MPTT – traverzování kolem stromu. Rovnou se podíváme i na reálnou implementaci tak, jak ji můžete použít ve svých projektech.
Seriál: Ukládáme hierarchická data v databázi (3 díly)
- Ukládáme hierarchická data v databázi – I 5. 3. 2012
- Ukládáme hierarchická data v databázi – II 14. 3. 2012
- Ukládáme hierarchická data v databázi – III 19. 3. 2012
Nálepky:
Tento článek je volným překladem anglického originálu vydaného na portálu SitePoint.
Podívejme se dnes na druhou metodu ukládání stromů. Rekurze může být pomalá, takže ji nechceme použít. Také bychom rádi minimalizovali počet dotazů na databázi – ideálně tak, aby pro jednu aktivitu existoval jeden dotaz.
Začneme tím, že si strom překreslíme do jiné podoby – jako kdybychom ho kreslili na papír. Začneme u hlavního uzlu („Jídlo“) a napíšeme 1 na jeho levou stranu. Budeme pokračovat na prvního potomka a napíšeme 2 vedle něj. Touto cestou „jdeme kolem stromu“ (pozn. překl: v angličtině traverse – v překladu „překračovat“, proto pro tento typ používám název „traverzování kolem stromu“.) Při procházení stromu píšeme čísla nejdříve na levou stranu a vždy, když jsme na nejspodnější části, přecházíme na pravou stranu – poslední číslo je napsané na pravou stranu uzlu „jídlo“. Níže můžete vidět obrázek s celým očíslovaným stromem:
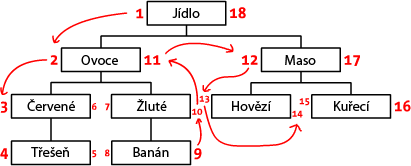
Nazveme tahle čísla jako „left“ a „right“ (levá a pravá). Jak můžete vidět, tahle čísla indikují vztah mezi každým uzlem stromu. Protože „červené“ má čísla 3 a 6, je potokem uzlu Jídlo, který má čísla 1–18. Stejně tak můžeme říct, že všechny uzly s levým číslem větším než 2, které mají pravé číslo menší než 11, jsou potomkem uzlu 2–11 „Ovoce“. Díky tomu můžeme zjednodušit dotazy na databázi a tento způsob se jmenuje „Modified preorder tree traversal“, tedy MPTT.
Pozn. překl.: jak bude uvedeno níže v článku, nejsem zastáncem ani jednoho ze způsobů – mám rád jejich kombinaci s doplněním parametru „level“ – tedy úrovně ve stromu. Všechny příklady v tomto a dalším díle budou vycházet z tohoto předpokladu, ačkoli pro funkci samotného MPTT stačí udržovat pouze údaje left a right.
Podívejme se tedy, jak bude vypadat naše databáze:
id parent left right level title 1 1 18 1 Jídlo 2 1 2 11 2 Ovoce 3 2 3 6 3 Červené 4 2 7 10 3 Žluté 5 3 4 5 4 Třešeň 6 4 8 9 4 Banán 7 1 12 17 2 Maso 8 7 13 14 3 Hovězí 9 7 15 16 3 Kuřecí
(strukturu databáze lze nalézt v příkladech v souboru mptt.sql)
Nezapomínejme, že „left“ a „right“ mají speciální význam v SQL. Proto nesmíme zapomínat na escape sekvenci MySQL – v dibi (a tím pádem i příkladech) ji ale používáme stejně, znaky [ a ].
Získáme strom
Pokud chceme získat celý strom, pak můžeme klasicky rekurzivně postupovat pomocí parametru parent. Díky MPTT nám ale k tomu bude stačit jeden SQL příkaz, který nám získá pouze položky, které mají parametr left mezi 2 a 11, tedy:
SELECT * FROM `mptt` WHERE `left` BETWEEN 2 AND 11;
Což vrátí:
id parent left right level title 2 1 2 11 2 Ovoce 3 2 3 6 3 Červené 4 2 7 10 3 Žluté 5 3 4 5 4 Třešeň 6 4 8 9 4 Banán
No, a tady to máme – celý strom v jednom dotazu. Nicméně abychom zobrazili strom, stejně jako jsme to udělali v naší rekurzivní funkci, budeme muset přidat klauzuli ORDER BY – použijeme parametr left, který nám k tomuto účelu perfektně postačí:
SELECT * FROM `mptt` WHERE `left` BETWEEN 2 AND 11 ORDER BY `left`;
Jediný problém je otevírání a uzavírání tagů <ul> – a k tomu se nám právě perfektně hodí parametr level. Pozn. překl: rovněž lze použít sekvenční zobrazování s tím, že si udržujeme frontu pravých hodnot. K účelům, které používá autor původního článku, to bohatě stačí – nicméně zastávám názor, že každý programátor, který k MPTT přijde, by ho měl umět používat více méně automaticky s trochou logiky a přemýšlení. Výsledkem je, že jsme v našich implementacích začali používat parametr level, čistě proto, že je pak vše jasnější.
function display_tree($id = null) {
// Nejdříve si získáme uzel, pro který chceme zobrazit děti. Pokud je ID
// NULL, pak chceme získat celý strom od "shora"
$query = dibi::select('*')->from('mptt');
if($id === null) {
$query->where('[parent] IS NULL');
}
else {
$query->where('[id] = %i', $id);
}
$root = $query->fetch();
if(!$root) {
return;
}
// A teď si získáme všechny potomky
$children = dibi::fetchAll('SELECT * FROM [mptt] WHERE [left] BETWEEN %i AND %i ORDER BY [left]', $root['left'], $root['right']);
// Pro ne-rekurzivní zobrazení si budeme udržovat aktuální "level"
$level = -1;
// A postupně zobrazíme děti
foreach($children as $one) {
// Ukončíme otevřené <ul> a <li> tagy
if($one['level'] < $level) {
$dismiss = $level - $one['level'];
for($i = 0; $i < $dismiss; ++$i) {
echo '</li></ul>';
}
}
// Ukončujeme aktuální <li>?
if($one['level'] == $level) {
echo '</li>';
}
// Máme zobrazit tag <ul>?
if($one['level'] > $level) {
echo '<ul>';
}
echo '<li>' . $one['title'];
$level = $one['level'];
}
// A nesmíme zaponemout uzavřít všechny otevřené tagy
for($i = $level+1; $i >= $root['level']; --$i) {
echo '</li></ul>';
}
}
Po jejím spuštění bychom měli vidět něco podobného následujícímu:

Cesta k uzlu
S algoritmem MPTT můžeme také jedním dotazem získat drobečkovou navigaci (cestu) k danému uzlu stromu. Pomocí left a right to není ani raketová věda: například, pokud chceme získat cestu k třešni, můžete se podívat, že všechny rodiče mají levé id menší než 4 a zároveň pravé id větší než 5. Použijeme tedy následující dotaz:¨
SELECT * FROM `mptt` WHERE `left` < 4 AND `right` > 5 ORDER BY `level` ASC;
Dotaz nám vrátí následující výsledek:
id parent left right level title 3 2 3 6 3 Červené 2 1 2 11 2 Ovoce 1 1 18 1 Jídlo
Pozn. překl.: Pro jednoduchost opět používáme atribut level, nicméně stejné funkčnosti lze dosáhnout i s použitím třídění podle parametru left.
Kolik je položek v kategorii
Pokud bychom potřebovali získat počet potomků, pak nám stačí jednoduchá aritmetika mezi left a right parametrem: prostě je od sebe odečteme, a vydělíme 2. Každý uzel stromu totiž přičte k celkovému počtu 2. Stačí nám tedy následující rovnice:
$count = ($node['right'] - $node['left'] - 1) / 2;
Přepočítáváme strom
Jednou za čas, například ve chvíli, kdy se rozhodnete MPTT implementovat do vašeho již běžícího projektu, potřebujeme funkci, která vezme nejvyšší uzel stromu a přepočítá všechny dílčí uzly. A zde se právě dostáváme k tomu, proč jsem v příkladech nechal parametr parent:
function rebuildTree() {
$root = dibi::fetch('SELECT * FROM [mptt] WHERE [parent] IS NULL');
if (!$root) {
return;
}
// Pošleme parametr $left jako 1, tedy první položku stromu
_rebuildTreeWorker($root, 1);
}
/**
* Actually rebuild the tree
*/
function _rebuildTreeWorker($parent, $left, $level = NULL, $output = false)
{
$right = $left + 1;
if ($level === NULL) {
$level = (int)$parent['level'];
}
$children = dibi::fetchAll('SELECT * FROM [mptt] WHERE [parent] = %i', $parent['id']);
foreach ($children as $row) {
$right = _rebuildTreeWorker($row, $right, $level + 1, $output);
}
$update = array(
'left' => $left,
'right' => $right,
'level' => $level,
);
dibi::update('mptt', $update)->where('[id] = %i', $parent['id'])->execute();
return $right + 1;
}
Ano, toto je rekurzivní funkce – ve skutečnosti používáme dvě. První si najde nejvyšší bod uzlu a spustí na něj funkci, která fyzicky prochází stromem. Ta si vždy najde veškeré děti a vrátí novou pravou hodnotu. Nakonec ji nastaví i u rodičovského uzlu.
Pokud nejsou žádné položky ve stromu, kromě té nejvyšší, nastaví rodičovskému uzlu 1 a jako pravou hodnu +1, tedy 2.
Díky rekurzi se funkce tváří složitější než vypadá – ve skutečnosti ale dělá přesně to, co jsme na začátku udělali ručně na papíře. Prochází kolem stromu a přidává 1 ke každému uzlu, který uvidí. Vyzkoušejte a uvidíte, že ve skutečnosti všechna čísla i po jejím spuštění zůstala stejná. Rychlá kontrola – hodnota right by měla být dvojnásobkem počtu uzlů.
Přidávání položek do stromu
Jak automatizujeme přidávání položek do stromu? Jsou dva přístupy: můžeme prostě přidat položku do stromu a celý strom následně přepočítat pomocí funkce rebuildTree() – jednoduché, ale ne příliš elegantní řešení; nebo můžeme aktualizovat levé a pravé hodnoty na všech uzlech, které jsou napravo od uzlu, který přidáváme.
První volba je jednoduchá, ale ne příliš efektivní s velkými stromy: prostě přidáte nový uzel, který bude mít správný parametr parent a ostatní (left, right, level) necháte nastavené na 0. Poté přepočítáte strom a vše je v pořádku.
Druhá cesta k přidávání a odebírání uzlů je nejdříve přepočítat všechny položky napravo od uzlu. Udělejme si příklad, kdy chceme přidat nový uzel „Jahoda“ pod červené ovoce. Nejdříve budeme muset udělat místo: pravá hodnota „Červené“ musí být změněna z 6 na 8, uzel 7–10 by měl být 9–12 atp. Aktualizace uzlu „Červené“ znamená, že budeme přidávat hodnotu 2 pro všechny uzly, kde je hodnota větší než 5.
UPDATE `mptt` SET `right` = `right` + 2 WHERE `right` > 5; UPDATE `mptt` SET `left` = `left` + 2 WHERE `left` > 5;
Teď můžeme přidat novou položku do uzlu. Tento bod musí mít hodnoty 6 a 7:
INSERT INTO `mptt` (`parent`, `left`, `right`, `level`, `title`) VALUES ('3', '6', '7', '4', 'Jahoda');
Teď spustíme funkci displayTree() a podíváme se, zda se uzel přidal správně:

Pokud chceme položku smazat, pak použijeme stejný přístup jako když ji přidáváme – jen v update místo přičítání použijeme znaménko -.
Nevýhody
Napoprvé může MPTT vypadat složitě. Je skutečně složitější než klasická metoda s ukládáním pouze pomocí parent. Nicméně, jakmile si zvyknete na hodnoty left a right velmi rychle poznáte, že s tímto modelem můžete dělat vše co s klasickou metodou – s tím, že tato metoda je mnohem rychlejší. Aktualizace stromu se skládá z více SQL dotazů, což je pomalejší, ale získávání stromu je mnohem rychlejší díky použití pouze jednoho dotazu a cyklu bez rekurze.
Příští díl
V příštím díle si ukážeme, jak jsme celé MPTT implementovali ve společnosti WDF před třemi lety. V rámci WDF se tyto stromy používají dodnes, i když prošli pár úpravami. Narazili jsme totiž na implementační chyby, tak na další aspekty MPTT, které vylezou na povrch až když máte 500 000+ položek v jednom stromu. Nicméně na to, jak jsme si s nimi poradili, si ještě chvilku počkejte.
Další čtení v angličtině
More on Trees in SQL by database wizard Joe Celko: http://searchdatabase.techtarget.com/…7290,00.html
Two other ways to handle hierarchical data: http://www.evolt.org/…7/index.html
Xindice, the ‘native XML database’: http://xml.apache.org/xindice/
An explanation of recursion: http://www.strath.ac.uk/…on3_9_5.html




Zdravím,
tento systém mi přijde poněkud zbytečně komplikovaný...Osobně to u svého systému řeším trochu jednodušeji. Mám v jedné tabulce uloženy záznamy s jejich pořadím a hloubkou vzhledem ke kořeni. V druhé tabulce je ID záznamu, ID jeho rodiče a hloubka vzhledem k tomuto rodiči. Tím pádem mohu jednoduše s použitím vnitřního spojení získat všechny potomky jakéhokoli záznamu na jakékoli hloubce. A navíc zpětně mohu získat také všechny rodiče jakéhokoli záznamu.
Pořadí a zanoření záznamů je určeno sloupci pořadí a hloubky v tabulce se záznamy.
Při vložení nového záznamu na určité místo stačí jen posunout pořadí všech následujících záznamů, vložit s požadovaným pořadím a aktualizovat tabulku spojení. S použitím indexů by měla být efektivita výběru prvků velmi dobrá.
Zdarec.
Nešlo by přidat k výpisům dat nějaké rozumné formátování?
A také zvýrazňování SQL syntaxe?
Bylo by to fajn :-)
Tomuhle se říká „Nested Intevals“. Je to velice chytrý, celkem a jednoduchý a při malém množství změn i velmi rychlý způsob, jak udržet strom v SQL databázi.
Rozhodně doporučuju nespoléhat jen na sloupce Left a Right, ale udržovat si i Parent, protože když se to povede rozbít (což se během vývoje může lehce stát), tak se to nedá jinak opravit.
Btw, pro MySQL existuje pěkný návod tu: http://web.archive.org/web/20110606032941/http://dev.mysql.com/tech-resources/articles/hierarchical-data.html (originál nějak zmizel z http://dev.mysql.com/tech-resources/articles/hierarchical-data.html)
Úplně ideální je ukládat si jak parent, tak level (např. vypsat celý strom, ale max. do třetí úrovně – do menu – zbytek bude jen v breadcrumbs) a využívat to při selectech.
A pokud probíhají časté úpravy do DB a DB neni moc velká, tak je jednodušší než dělat updaty nad MPTT upravit jen parent/level a pak přepočítat celý strom rekurzivně.
Používám to ve svém projektu na eshopu s přibližně 100 kategoriemi a funguje to v pohodě. Celé přegenerování trvá nějakých slabých 250ms. Což je docela dost, ale při jednorázové akci, jakou změna v kategoriích je to není takový problém.
Díky, dlouho jsem hledal ten původní článek, který byl najednou 404.
Na diskuzi je vidět jeden podstatný nedostatek celého článku: není příliš zřejmé, jaké operace chceme nad stromem provádět. Každá reprezentace bude mít svoje výhody pro podporu určitých operací. Například pro vypsání stromu je intervalové hodnocení skutečně zbytečné (te to vidět i na tom, že algoritmus display_tree používá pouze left hodnotu).
Jak jsem psal už u minulého dílu: je to jako by jste řešili jaký bude nejlepší dům, ale jaksi zapoměli zmínit k čemu bude sloužit.
Souhlas – a taky záleží na počtu uzlů, alespoň orientačně – je dost velký rozdíl, jestli jich máme 100 (např. kategorie zboží v obchodě) nebo milion. V prvním případě není žádný problém držet v RAM sestavený strom (třeba jako XML DOM) a z databáze číst jen při změnách (jak často přibývají kategorie v obchodě?). S rostoucím počtem uzlů a frekvencí změn to problém začíná být a je potřeba hledat jiné řešení.
Další věc je nějaké vnitřní členění stromu – zatím se tu píše o obecných stromech a univerzálních řešeních, ale může to být tak, že některé části stromu patří k sobě a pak se vyplatí dělat něco jako „partitioning“. Např. u diskusních příspěvků nás bude zajímat obvykle jedna diskuse jako celek – ne všechny příspěvky z celého serveru jako jeden strom a ne jedno podvlákno (to jen výjimečně). Proto může být rozumné držet si u všech příspěvků vedle jejich předka i odkaz na článek (diskusi), ke kterému patří, protože obvykle budeme provádět operace nad příspěvky z této skupiny. (denormalizovaná databáze)
No vidite a to jste jeste zapomel treba mutace, a dalsi moznosti jak charakterizovat pripadne podmnoziny stromů. Asi nema smysl to vsechno rozepisovat ne?
Osobně jestě volím navíc artibut tree_id. Ten mu umožnuje držet více stromů vedle sebe, v jedné tabulce, s více root elementy.
Zasvědcení jistě budou znát aplikace django-mptt, která vše zmíněné obsahuje.
Ještě je dobrá dát si pozor při přesouvání (patrně obsah příštího článku) na „kauzální“ problémy – přesun rodiče pod svého potomka…
Ještě doplním link:
https://github.com/django-mptt/django-mptt
musím tedy souhlasit s různými příspěvky v nichž padlo a nebo z nich vyplíva ze implementace je urcena vetsinou pozadavky. A nebo delame neco robusnejsiho, vsestranejsiho, to by pak melo obsahovat vetsi miru abstrakce.
http://blog.voracek.net/databaze/closure-table-stromy-v-mysql-trochu-jinak/
nenacitaji se obrazky. Upravit pravopis . Zvyraznovat kod