WebGL: Šrouby a matice

Když jsem se před časem poprvé ponořil do světa WebGL, začínal jsem na zelené louce. Kdybych chtěl mít rychle nějaký výstup, jistě bych šáhnul po hotovém řešení, poskytujícím přímo graf scény (například vynikající three.js). Já chtěl ale vědět, jak a proč ty věci fungují; každou funkci si vyzkoušet a pochopit její účel. Své poznatky budu sepisovat, kdyby se náhodou někomu hodily…
Seriál: Začínáme s WebGL (5 dílů)
- Vytváříme Hello World pro WebGL 15. 5. 2013
- WebGL: Milostný RGB trojúhelník 22. 5. 2013
- WebGL: Šrouby a matice 29. 5. 2013
- WebGL: Darth Shader 5. 6. 2013
- WebGL: Texturovat, nemíchat 12. 6. 2013
Nálepky:
Po předchozích dvou částech seriálu už pro nás WebGL není nic tajemného: známe význam a funkci shaderů, používáme buffery, kreslíme body a čáry, chápeme rozdíl mezi souřadnicemi bodu a indexem. Dnes přišel čas pokročit na třech frontách zároveň:
- Začneme vykreslovat trojúhelníky
- Body umístíme do prostoru
- Výsledným objektem budeme otáčet (tj. animovat)
Cílem bude jeden z nejprostších prostorových útvarů, čtyřstěn. Zdrojového kódu už máme nehezky hodně, pojďme tedy ukázky rozdělit s ohledem na výše vytyčené mezikroky.
Bod, čára a konečně nějaká plocha
Čtyřstěn je trojboká pyramida, má čtyři vrcholy a každý z nich má tři (prostorové) souřadnice. Pojďme tedy naše geometrická data nacpat do bufferu o dvanácti prvcích:
var vertices = [
0.0, 1.0, 0.0, // "nahore"
0.0, 0.0, -1.0, // "vzadu"
1.0, -1.0, 1.0, // "vpravo"
-1.0, -1.0, 1.0 // "vlevo"
];
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(vertices), gl.STATIC_DRAW);
gl.vertexAttribPointer(posLoc, 3, gl.FLOAT, false, 0, 0);
Nově do atributu pos ve vertex shaderu již posíláme trojice čísel (druhý parametr pro vertexAttribPointer) a tím pádem upravíme i kód shaderu:
attribute vec3 color;Budeme také potřebovat čtyři barvy pro čtyři vrcholy:
var colors = [
1.0, 0.0, 0.0,
0.0, 1.0, 0.0,
0.0, 0.0, 1.0,
1.0, 1.0, 0.0
];
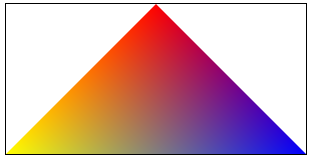
A celou pyramidku vykreslíme opět metodou drawElements, ovšem tentokrát budou geometrická primitiva trojúhelníky:
gl.drawElements(gl.TRIANGLES, indices.length, gl.UNSIGNED_BYTE, 0);Výsledná ukázka je k vidění na http://jsfiddle.net/ondras/YMZfW/.
Transformace bez legrace
Přišel čas ponořit se do problematiky transformace souřadnic bodů. V praxi budeme chtít naše geometrické prvky v prostoru přesouvat, zvětšovat a zmenšovat, natáčet. Těmto úpravám se říká afinní transformace a pokud na bod v prostoru nahlížíme jako na N-rozměrný vektor, jeho afinní transformaci lze realizovat násobením vhodnou maticí. Pokud tedy pro námi vybranou transformaci dokážeme získat matici (v jejíž hodnotách je transformace zakódována), můžeme body maticí násobit a tím získávat nové souřadnice. Ještě zajímavější je, že více různých transformací (každá má svoji matici) lze zkombinovat do jedné (tím, že jejich matice navzájem vynásobíme). Můžeme si tedy v jedné matici pamatovat celou řadu různých operací a provádět je pak naráz.
Zajímavost: Násobit lze vždy vektory a matice stejných velikostí, tj. N-rozměrný vektor násobíme maticí N×N. Náš trojrozměrný vektor tedy násobíme maticí 3×3, což odpovídá lineární transformaci (změně velikosti a natočení). Pokud chceme ještě body posouvat, musíme použít matici 4×4. Pro tu ale zase potřebujeme čtyřrozměrný vektor: ten získáme přidáním jedničky k našemu existujícímu trojrozměrnému.
Implementace maticových operací není složitá, ale můžeme si usnadnit práci a sáhnout po nějaké hotové (a otestované) maticové knihovně. Nabídka je poměrně široká; já osobně mohu doporučit glMatrix a tento tip podložit následující argumentací:
- glMatrix nenabízí vlastní datové typy, ale operuje přímo nad nativními (Float32Array nebo Array).
- Výsledkem maticových a vektorových operací nejsou nové objekty, takže nedochází ke zbytečné alokaci.
- Data jsou ukládána do jednorozměrných polí, takže kompletně odpadá jakýkoliv flattening. Pokud předáváme matici do WebGL, nemusíme ji pro tento účel nijak transformovat či serializovat.
- Nabízená nomenklatura koresponduje s názvy typů a funkcí v GLSL (vec{2..4}, mat{2..4}).
Drobnou nevýhodou je na první pohled nezvyklá syntaxe, kdy všechny funkce připomínají spíše statické metody, které jako první parametr přijímají výstupní objekt. V dalších ukázkách na jsFiddle bude knihovna glMatrix implicitně používána.
Model, View, Controller Projection
Pomocí matic bychom mohli naše souřadnice transformovat dle potřeby. Pokud bychom pak ale chtěli například objekt periodicky otáčet, museli bychom při každém otočení měnit hodnoty všech vrcholů a stále dokola je nahrávat do paměti grafické karty (bufferData). Namísto toho je zvykem, že všechny relevantní transformace předáme ve formě matic do vertex shaderu, který provede maticové násobení a následně pracuje s již upravenými souřadnicemi.
Tradičně pro tento účel používáme tři matice se standardním označením. Model matrix je transformace, kterou držíme pro každý vykreslovaný objekt a ten s její pomocí transformujeme. Náš čtyřstěn tak může být definován jako v první ukázce (jedničkové rozměry, umístěný kolem počátku souřadné soustavy) a následně jej podle potřeby díky model matrix natočíme, zmenšíme či posuneme tam, kde jej potřebujeme.
View matrix je druhá transformace, kterou na renderované prvky aplikujeme. V OpenGL neexistuje žádný koncept „kamery“; vzájemný vztah scény a jejího pozorovatele realizujeme právě násobením touto maticí. Pokud máme tedy rozmístěno mnoho objektů a chceme je všechny od pozorovatele oddálit, násobíme jejich vrcholy view matrix, která koresponduje s posunem ve směru osy Z.
Poslední tradiční maticí je Projection matrix; transformace, která provádí nějakou formu perspektivního zkreslení. V našich ukázkách jsme zatím perspektivu ignorovali a při projekci (tj. převodu z 3D do 2D canvasu) třetí souřadnici prostě zahodili. Pokud chceme nabídnout něco lepšího, můžeme požadované zkreslení definovat jako třetí matici.
Abychom mohli do vertex shaderu tyto tři matice předat, musíme se seznámit s dalším druhem parametrů shaderu: bokem proměnných attribute (jejichž hodnota se mění pro každý vrchol geometrie) a varying (které slouží pro interpolaci hodnot mezi vertex a fragment shaderem) máme k dispozici ještě typ uniform, kterým označujeme data, jejichž hodnoty se během jednoho vykreslení scény nemění. Pokud si některou ze tří uvedených transformací nepřejeme provádět, použijeme jednotkovou matici – ta odpovídá násobení jedničkou, tj. no-op.
Od slov k činům
Druhá ukázka na http://jsfiddle.net/ondras/LLVPx/ již používá glMatrix a MVP matice ve vertex shaderu. Jaké úpravy jsme provedli?
Přidali jsme matice jako uniform proměnné do vertex shaderu a při výpočtu pozice s nimi vynásobili souřadnice právě zpracovávaného vrcholu:
uniform mat4 MMatrix;
uniform mat4 VMatrix;
uniform mat4 PMatrix;
...
gl_Position = PMatrix * VMatrix * MMatrix * vec4(pos, 1.0);
Vyrobili jsme Model matrix, která reprezentuje změnu měřítka (v každé ose jinak):
var mmatrix = mat4.create();
mat4.scale(mmatrix, mmatrix, vec3.fromValues(0.5, 0.8, 0.8));
Tuto matici jsme předali do vertex shaderu metodou uniformMatrix4fv:
var mmLoc = gl.getUniformLocation(program, "MMatrix");
gl.uniformMatrix4fv(mmLoc, false, mmatrix);
Vposled jsme do shaderu poslali ještě matice View a Projection, které ale necháváme na výchozích hodnotách, tj. jednotkové:
var vmLoc = gl.getUniformLocation(program, "VMatrix");
gl.uniformMatrix4fv(vmLoc, false, mat4.create());
var pmLoc = gl.getUniformLocation(program, "PMatrix");
gl.uniformMatrix4fv(pmLoc, false, mat4.create());
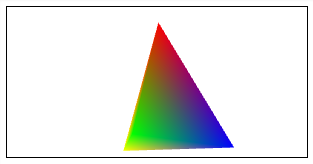
Ve výsledku (http://jsfiddle.net/ondras/LLVPx/) se mnoho nezměnilo, jen je vykreslovaný čtyřstěn zmenšený. Jsme ale nachystáni na poslední krok, totiž průběžné transformování v rámci animace.
Pohyblivé obrázky
Poslední kapitolou dnešního dílu je rozpohybování celého objektu. Znamená to v nekonečné smyčce měnit transformační matici (model matrix) a pořád dokola překreslovat scénu. Mohli bychom použít tradiční setInterval, ale vhodnější bude sáhnout po modernější alternativě, totiž funkci requestAnimationFrame, která automaticky volí vhodný čas na spuštění (cílí zpravidla na 60 FPS, ale záměrně vykonává callback tak, aby to lépe zapadal do vykreslovací pipeline celého prohlížeče). requestAnimationFrame je často prefixovaná a není dostupná ve všech prohlížečích, vytvoříme si proto triviální polyfill:
window.requestAnimationFrame = window.requestAnimationFrame
|| window.mozRequestAnimationFrame
|| window.webkitRequestAnimationFrame
|| function(cb) { setTimeout(cb, 1000/60); };
Vykreslení zabalíme do vlastní funkce render, která bude nepřímo (pomocí requestAnimationFrame) volat sama sebe. V každé iteraci navíc adekvátně upravíme matici mmatrix, v našem případě přidáním otočení v osách X a Y (rotateX, rotateY):
var render = function() {
mat4.rotateX(mmatrix, mmatrix, 0.01);
mat4.rotateY(mmatrix, mmatrix, 0.03);
gl.uniformMatrix4fv(mmLoc, false, mmatrix);
gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);
gl.drawElements(gl.TRIANGLES, indices.length, gl.UNSIGNED_BYTE, 0);
requestAnimationFrame(render);
}
Poslední ingrediencí je vyřešení problému s hloubkou. Při volání drawElements se totiž vykreslí veškerá primitiva v pořadí, ve kterém jsou definována v bufferu. V našem případě jsou trojúhelníky ve „správném“ pořadí, tj. ten přední až na konci překryje všechny předchozí. Jakmile ale objekt začneme natáčet, dostaneme se do problémů s překryvem trojúhelníků. OpenGL pro tuto situaci naštěstí poskytuje snadný nástroj – testování hloubky. Do bufferu bokem (tzv. depth buffer) si ukládá hloubku (souřadnici Z) jednotlivých bodů; porovnáním s již vykreslenými pixely pak rozhodne o zahození těch, které by měly zůstat neviditelné „vzadu“. Pro nás to znamená dvě triviální úpravy: vymazání tohoto bufferu v každé iteraci (gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT)) a také zapnutí testování hloubky (ve výchozím nastavení se totiž neprovádí):
gl.enable(gl.DEPTH_TEST);Výsledný otáčející se útvar lze shlédnout na adrese http://jsfiddle.net/ondras/DLPeb/.
To je pro dnešek vše; v příštím díle se seznámíme s perspektivou, normálami a základy osvětlení. Archiv se všemi ukázkami tohoto dílu je k dispozici ke stažení.




Pekný článok. Inak v tom poslednom príklade je pekne vidno ako sa časť rohu pri otáčaní nevykreslí lebo je mimo scény
Zdravim, skusal som v prvom priklade http://jsfiddle.net/ondras/YMZfW/ doplnit depth test:
a zeleny (druhy) bod sa vykresluje vpredu, namiesto vzadu.
Mate pravdu, zeleny bod ma spatny popisek – clipspace pouziva opacnou orientaci osy Z, zeleny bod je proto se zapornou souradnici blize uzivateli, nez body ostatni.
Doplnim, ze vice se o tom lze docist napriklad zde: http://stackoverflow.com/questions/17650219/when-is-z-axis-flipped-opengl